Quantum Spin Glasses with Nobel Prize Dr Giorgio Parisi

The project aims to connect a problem in fundamental physics (the dynamics of spin glasses at zero temperature, when the dynamics is dictated by a quantum transverse field) with the approach to quantum computation named Quantum Annealing.

On the one hand, the phase transition that a spin glass experiences upon varying the transverse field is still poorly known despite many years of intensive research on spin glasses. On the other hand, Quantum annealing holds the promise to solve Combinatorial Optimization problems better than any classical computer could. These problems are ubiquitous in everyday life, whenever many agents compete trying to achieve mutually contradicting goals and a reasonable compromise is needed (assigning resources in an organization is an obvious example). Finding the ground state for spin glasses provides an (almost) universal model of hard optimization problems. Therefore, most Quantum Annealing experiments attempt to solve spin glasses problem-instances.

A particular physical property at the phase-transition, named the energy gap, controls the complexity of solving a particular problem instance in a quantum annealer. Mutually contradicting predictions exist about how this gap will behave. Unfortunately, which of these alternatives (if any!) provides the correct picture is a very hard computational task. It also is the main objective of our project that employs custom CUDA codes. These codes need to be run on a large High Performance Computing facility such as MeluXina GPU, where a large number of high-end GPUs are available to the European Scientific Community through the EuroHPC program. Thanks to this combination of highly optimized codes and enormous computational power the team was able to reach unprecedented accuracy and reliable statistics that will deliver a clearer perspective than previously thought possible.

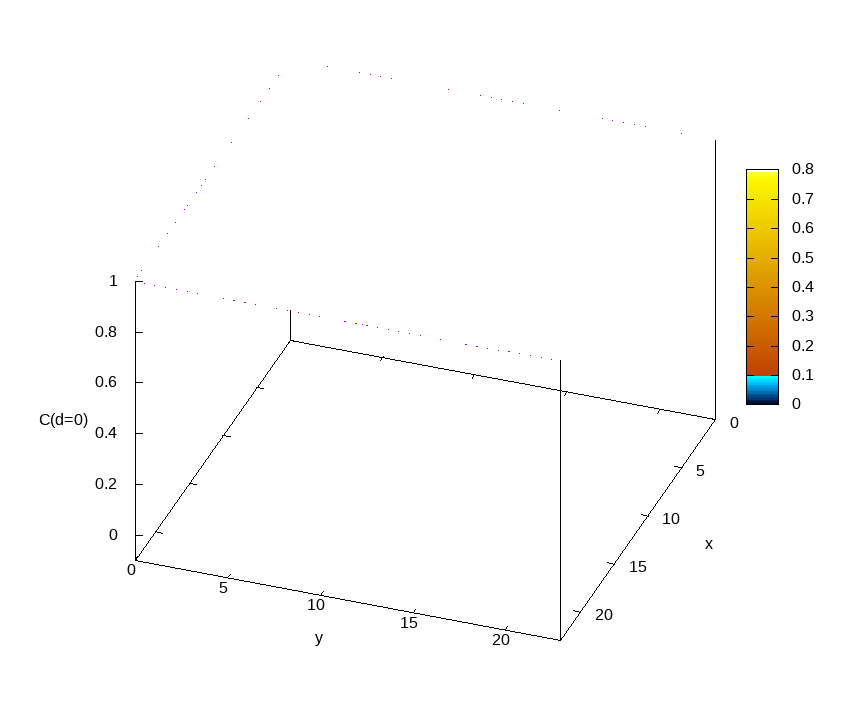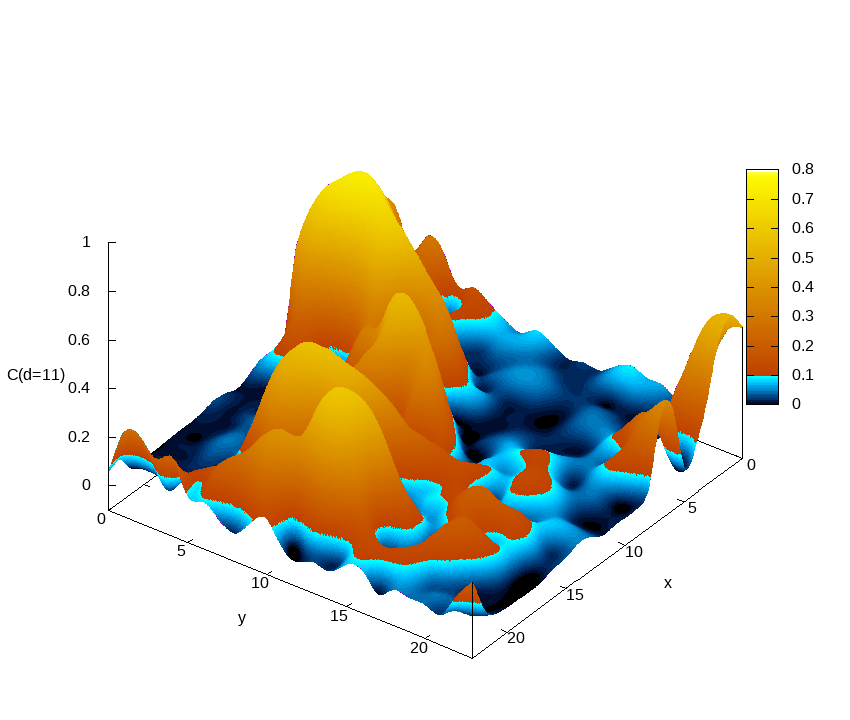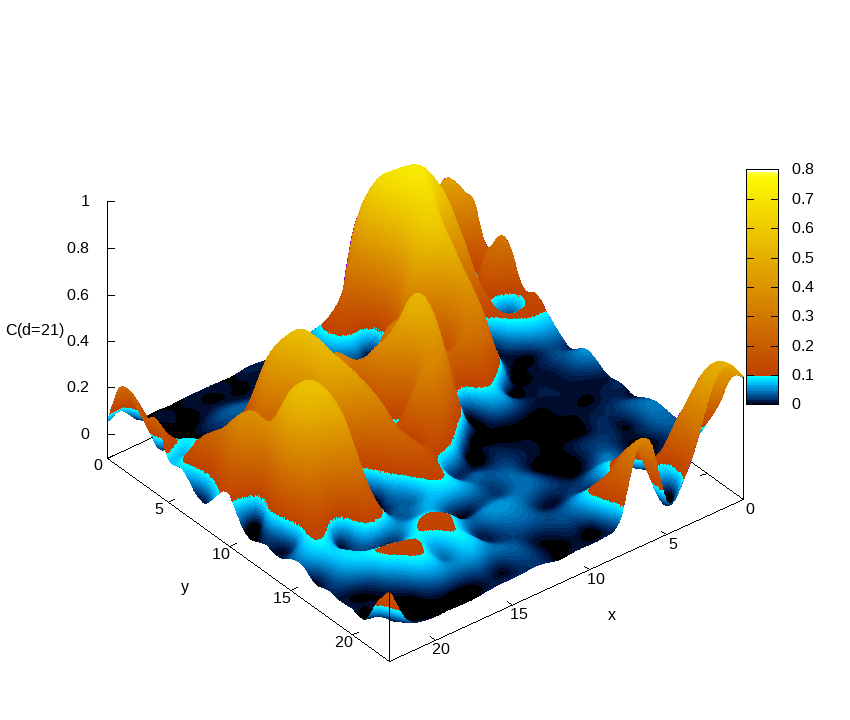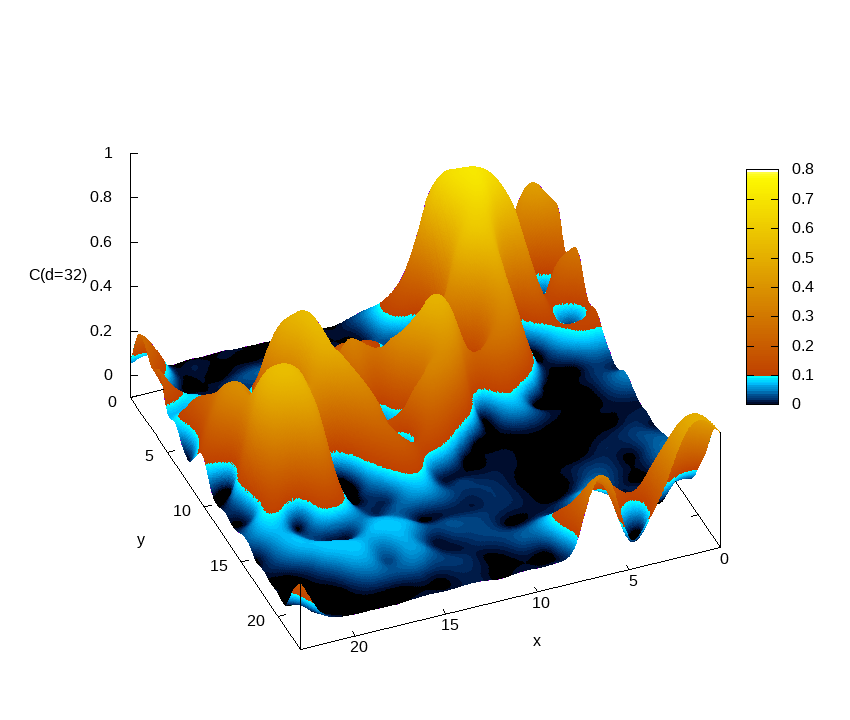
Euclidean correlation function

C(x,y,τ=d)=⟨σZ(x,y,0)σZ(x,y,τ=d)⟩

as computed on a sample of size 24x24x2048 at beta=0.292.

Different frames correspond to different Euclidean distances d. The correlation function at a given d is represented as a contour map. For all sites (x,y), the correlation function starts from one at tau=0 and decreases when tau increases. While for most sites C(x,y,tau) quickly becomes very small as tau grows,  for a few sites the correlations survive for very long times. These minority sites are responsible for the small gaps that make these systems difficult to simulate. This is the main reason why we need to simulate a huge Euclidean length (L_tau=2048 in the case of the figure). This is only possible in an HPC facility with a great number of graphic accelerators (GPU) such as MeluXina.