
Exploring the Future of Trading with Quantum Reinforcement Learning on the MeluXina Supercomputer
Executive Summary
The growth of Quantum Computing and Quantum Reinforcement Learning (QRL) are on the brink of revolutionizing various sectors, including financial markets. They have emerged as a promising approach to improve efficiency, adaptability, and profitability in algorithmic trading strategies.
The paper proposes a way to conduct the experiment on historical financial data with a duration of 10 years and a recommendation of fine-tuned initial parameters for the setup on MeluXina, the National Supercomputing platform in Luxembourg. The paper debates the QRL algorithmic trading model’s trading performance across different risk assessment metrics including Returns on Investment (ROI), Sharpe Ratio, Sortino Ratio and Max Drawdown, explores its scalability and quantum advantages and review the limitations on Classical Reinforcement Learning (CRL) compared to QRL.
Introduction
Artificial Intelligence (AI) has changed the financial industry by automating trading decisions using predefined rules. The automated approach has benefits, including increased efficiency, the ability to analyze vast amounts of data in near real-time, and faster execution speeds. Using automated algorithms, traders can identify profitable opportunities, optimize portfolio allocation, and manage financial risks more effectively. Despite the adoption of AI in algorithmic trading, the dynamic nature of financial markets brings a significant challenge to traditional trading algorithmic strategies. Financial markets are complex systems with non-linear relationships, high volatility, and frequent changes. This complexity often hinders the ability of traditional algorithmic trading strategies to adapt to dynamic market conditions, leading to poor performance and increased risk exposure.
Traditional AI trading algorithms have limitations due to their inability to learn and adapt to changing market conditions. Reinforcement Learning (RL) has been applied to algorithmic trading to address the issue of adaptability to market volatility. RL allows trading agents to learn from its actions and rewards, enabling trading algorithms to improve its strategies. However, the RL algorithm may need faster convergence rates, limitless scalability, and the ability to capture the complex dynamics of financial markets.
Quantum computing yields an enormous potential to revolutionize algorithmic trading by leveraging the principles of parallelism and superposition in quantum mechanics, which allow it to process massive amounts of data simultaneously and solve complex problems faster than classical computers. Its ability to evaluate multiple strategies across different market conditions, record non-parametric correlations and patterns among various financial instruments, and search for optimal parameters exponentially faster provides professional traders with valuable insights and enhances decision-making. By processing vast amounts of market data at high speeds and capturing complex dynamics, quantum computing enables more accurate predictive modeling and simulations in finance.
QRL models prove that they can capture multidimensional relationships in financial data, enabling more accurate market forecasting and risk assessment. It uses quantum-enhanced Machine Learning (ML) techniques, such as quantum neural networks, to improve prediction capabilities and handle sophisticated trading scenarios. They present the benefits of exploring vast state spaces and exponentially faster computations. QRL improves algorithmic trading strategy’s adaptability, scalability, and profitability compared to the Classical RL approach [1][2][3].
Background
CRL (Classical Reinforcement Learning) faces limitations due to computational complexity and high-dimensional state spaces. Training a CRL, such as a Deep Q-Network, on high-dimensional input data including multiple investment assets and performance indicators like the Sharpe ratio, Sortino ratio, Max Drawdown, and market features such as trends, volatility, and sentiment is time-consuming and resource-intensive. Moreover, defining an appropriate reward function for a range of trading actions like hold, buy, and sell is crucial for RL agents to effectively learn the market and assess risks and opportunities.
In contrast, QRL (Quantum Reinforcement Learning) can possibly break down the above barriers and address the shortcomings in traditional RL approach by capitalizing on the advantages of quantum superposition and entanglement. This allows QRL to explore multiple trading strategies simultaneously, identifying more profitable strategies more quickly than CRL.
- Lack of comparisons between hybrid quantum-classical RL at scale
Although some comparisons have been made between classical and quantum approaches in machine learning in the literature, hybrid quantum-classical computing RL in the context of algorithmic trade is limited[4]. This gap makes it challenging to examine the benefits and limitations of hybrid quantum-classical RL for market-based financial data and multi-faceted trading scenarios.
- Need for benchmarking hybrid quantum-classical RL performance on High-Performance-Computing (HPC) architectures
The need for benchmarks on high-performance, robust, and scalable infrastructure with high fault-tolerance like HPC or Supercomputing platform is crucial. Such infrastructure must provide the computational power and secure environment necessary to handle large, sensitive datasets and fine-tune trading strategies efficiently, without sacrificing the speed or low latency. Reliable and measurable benchmarking delivers practical insights that guide future research and development in the financial sector. Additionally, the performance comparison of hybrid quantum-classical RL algorithmic trading on high-performance computing architectures, such as GPUs and FPGAs, remains unexplored.
- Hybrid quantum-classical and HPC for algorithmic trading
This study recommends a hybrid quantum-classical approach by using quantum reinforcement learning with High-Performance-Computing for algorithmic trading. This approach leverages the advantages of quantum computing, such as entanglement and the benefits of HPC for scalability. It also provides the benefit of developing an efficient and profitable trading algorithm that can perform better than CRL.
A Proposal of Experimental Trading Setup on Supercomputer MeluXina
This section presents the experimental setup and results of QRL approach. The trading simulation and optimization are running on MeluXina, a national Supercomputer in Luxembourg, and exploring the performance on different compute modules: GPUs and FPGAs. The experiment aims to evaluate the performance of QRL agents within a simulated trading environment and compare their results with the actual stock returns.
- Hybrid QRL Experiment Setup on MeluXina
A custom trading environment is set up and the environment is initialized with a start date of ’2014-01-01’, an end date of ’2024-01-01’, and a transaction cost of 0.05%. Stock data is fetched using the ’SPX’ ticker symbol, representing a stock market index tracking the stock performance of 500 of the largest companies listed on stock exchanges in the United States. For the classic reinforcement learning, Deep-Q-Network (DQN) algorithm is used to train the model. DQN is a reinforcement learning algorithm that uses Deep Neural Networks with Q-learning to learn optimal policy. The training process uses DQN with experience replay, running for 500 episodes, including a 0.99 discount factor, epsilon-greedy exploration (starting at 1.0 and decaying to 0.01), and a replay memory of 1000 interactions. For training optimization, Adam optimizer is used, with varying learning rates for different model components. The agent’s action space is discrete, with three possible actions such as buy, hold, or sell, and a 5-dimensional state vector representing historical returns, and a reward system based on action outcomes and transaction costs. The same training parameters are set for QRL as CRL to train and test the agent, and a 5-qubit quantum circuit is used.
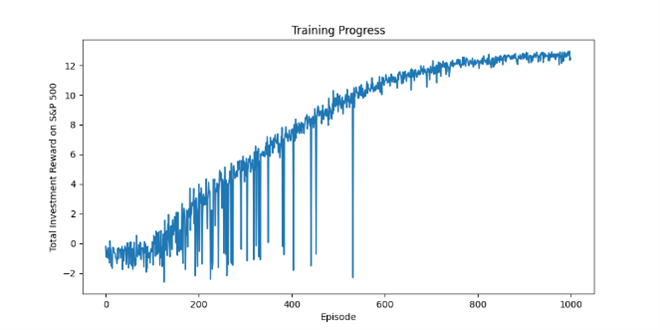
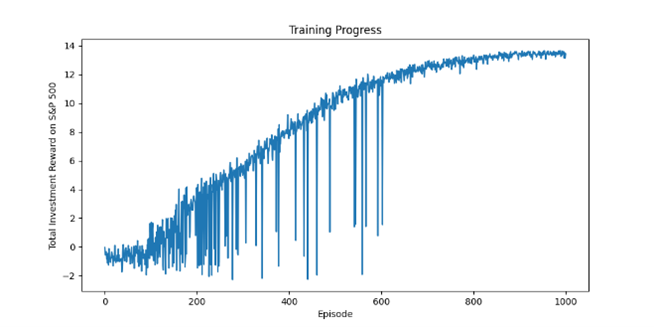
These graphs show the cumulative rewards obtained by QRL agents during each episode during the training process. This demonstrates the agent’s ability to learn and improve its trading strategy. The figure shows the average reward over the last ten episodes to track the agent’s
performance. After training, the QRL agent’s performance is compared with actual stock returns. The training algorithm is setup and run on FPGAs cluster and GPUs accelerators on Supercomputing Platform MeluXina.
- Diagram of Quantum Reinforcement-Learning with Deep-Q-Network

The figure shows one layer of algorithmic trading quantum circuit, which is repeated five times in the full model. The circuit has five qubit lines and uses single-qubit rotation gates (Rx, Ry, Rz) on each qubit. These rotations transform the input data to capture complex financial patterns for trading.
- Investment Rewards performed on GPUs and FPGAs Accelerator
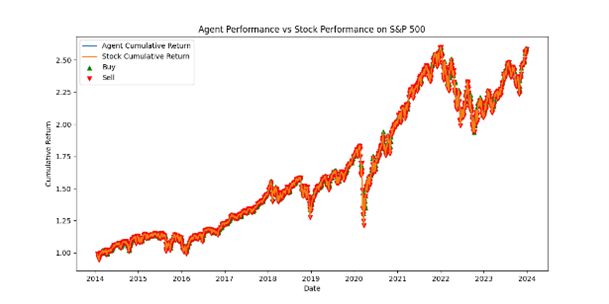
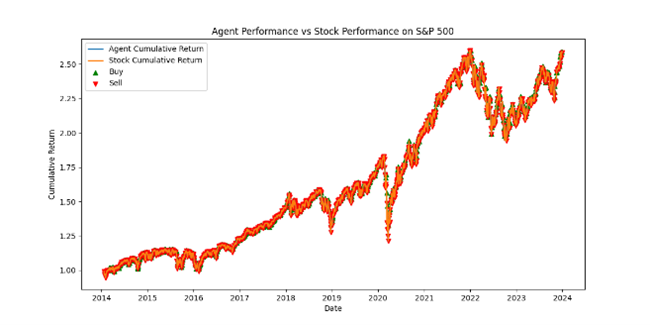
The cumulative returns of the agent and the actual stock are calculated and plotted in the above graphs. They illustrate the agent’s ability to make profitable trading decisions compared to the buy-and-hold strategy. In general, the graphs above show the trading in both environments performs better in the long run. Specifically, the loss is stopped in episode 500 for the experiment on GPUs and in episode 600 for the experiment on FPGAs. The trend demonstrates the algorithm performs more stable on GPUs than FPGAs with less dropping points from the starting point to approximately the middle of investment period. However, the reward gained on FPGAs and GPUs are steadily increased and starting at episode 400 to 1000, the algorithm on FPGAs outperforms the one on GPUs. Even though the difference is not significant, it can be concluded that with a long-term investment strategy, the result in FPGAs seems 2% better than GPUs.
- References
[1] Y. Qiu, Y. Qiu, Y. Yuan, Z. Chen, and R. Lee, “QF-Tradernet: Intraday Trading via Deep Reinforcement with Quantum Price Levels-based Profit-and-Loss control,” Frontiers in Artificial Intelligence, vol. 4, p. 749878,2021.
[2] C. Cheng, B. Chen, Z. Xiao, and R. S. Lee, “Quantum Finance and Fuzzy Reinforcement Learning-based Multi-agent Trading System,” International Journal of Fuzzy Systems, pp. 1–22, 2024.
[3] S. Y.-C. Chen, C.-H. H. Yang, J. Qi, P.-Y. Chen, X. Ma, and H.-S. Goan, “Variational Quantum Circuits for Deep Reinforcement Learning,” IEEE access, vol. 8, pp. 141 007–141 024, 2020.
[4] M. Moll and L. Kunczik, “Comparing Quantum Hybrid Reinforcement Learning to Classical Methods,” Human-Intelligent Systems Integration, vol. 3, no. 1, pp. 15–23, 2021.
[5] S. Jerbi, C. Gyurik, S. Marshall, H. Briegel, and V. Dunjko, “Parametrized Quantum Policies for Reinforcement Learning,” Advances in Neural Information Processing Systems, vol. 34, pp. 28 362–28 375, 2021.
[6] R. Lin, Z. Xing, M. Ma, and R. S. Lee, “Dynamic portfolio optimization via augmented ddpg with quantum price levels-based trading strategy,” in 2023 International Joint Conference on Neural Networks (IJCNN). IEEE, 2023, pp. 1–8
ABOUT THE AUTHORS




